Axion cosmic strings
Axion cosmic strings are hypothetical one-dimensional topological defects predicted in theories where the axion field—introduced to solve the strong CP problem in QCD—undergoes spontaneous symmetry breaking. They form as thin, line-like structures in the early universe, carrying quantized axion "winding" around them. These strings could radiate axions as they evolve, potentially contributing to the dark matter abundance. Networks of axion strings are expected to form, intersect, and decay over cosmic time. Detecting their signatures, such as gravitational waves or axion radiation, would provide key evidence for axions and new physics beyond the Standard Model.
We studied in this references string formation and dynamics in a scalar field theory with a global U (1) symmetry. If a scalar field Φ subject to a wine-bottle potential is initially displaced from the potential minimum, and even if this is done uniformly and coherently over large spatial patches, we show that small spatial perturbations to Φ grow through parametric resonance as Φ oscillates; this observation holds over a wide range of initial U (1) charge densities. We show that the growth of these perturbations leads to the formation of spatially coherent, temporally stable counter-rotating regions; i.e., spatially connected regions that exhibit Φ evolution with large and opposite-sign rotation speeds in field space and that persist over long durations. These counter-rotating regions are separated by domain boundaries characterized by a large field gradient and zero rotational speed in field space. We find that string or vortex topological defects form, are confined to, and then annihilate periodically on these domain boundaries. We demonstrate these periodic dynamics with numerical simulations in both 2 + 1 and 3 + 1 dimensions, in both Minkowski spacetime and in a radiation-dominated Friedmann–Lemaitre–Robertson–Walker (FLRW) universe, and we explain some features of the evolution (semi-)analytically. At late times in an expanding universe, when Φ approaches the minimum of the potential, we find counter-rotating regions and vortices to dissipate into scalar radiation. Phenomenologically, periodic bursts of string formation and annihilation are expected to lead to periodic bursts of gravitational-wave production. For small initial U (1) charge density, these gravitational-wave bursts can be synchronized across the whole Universe. Owing to their periodic nature, it is possible that they could give rise to a gravitational-wave frequency spectrum consisting of a forest of fully or partially resolved peaks. We find that these periodic scalar field dynamics also occur with large (but not fine-tuned) initial U (1) charge density; they may thus have implications for models that depend on a coherent field rotation, such as kination and the axion kinetic-misalignment mechanism.
Due to the non-vanishing rotation speed of the angular mode, a parametric resonance instability is triggered, if the radial mode is excited away from its minimum. Specifically, this resonance drives inhomogeneous spatial perturbations of a particular range of wavenumbers. These expontentially growing modes produce large gradients of the angular mode, which are ultimately sites of vortex string production. In the video below, an example of this resonance in the radial mode (left), angular speed (center), and angular mode (right) is shown:
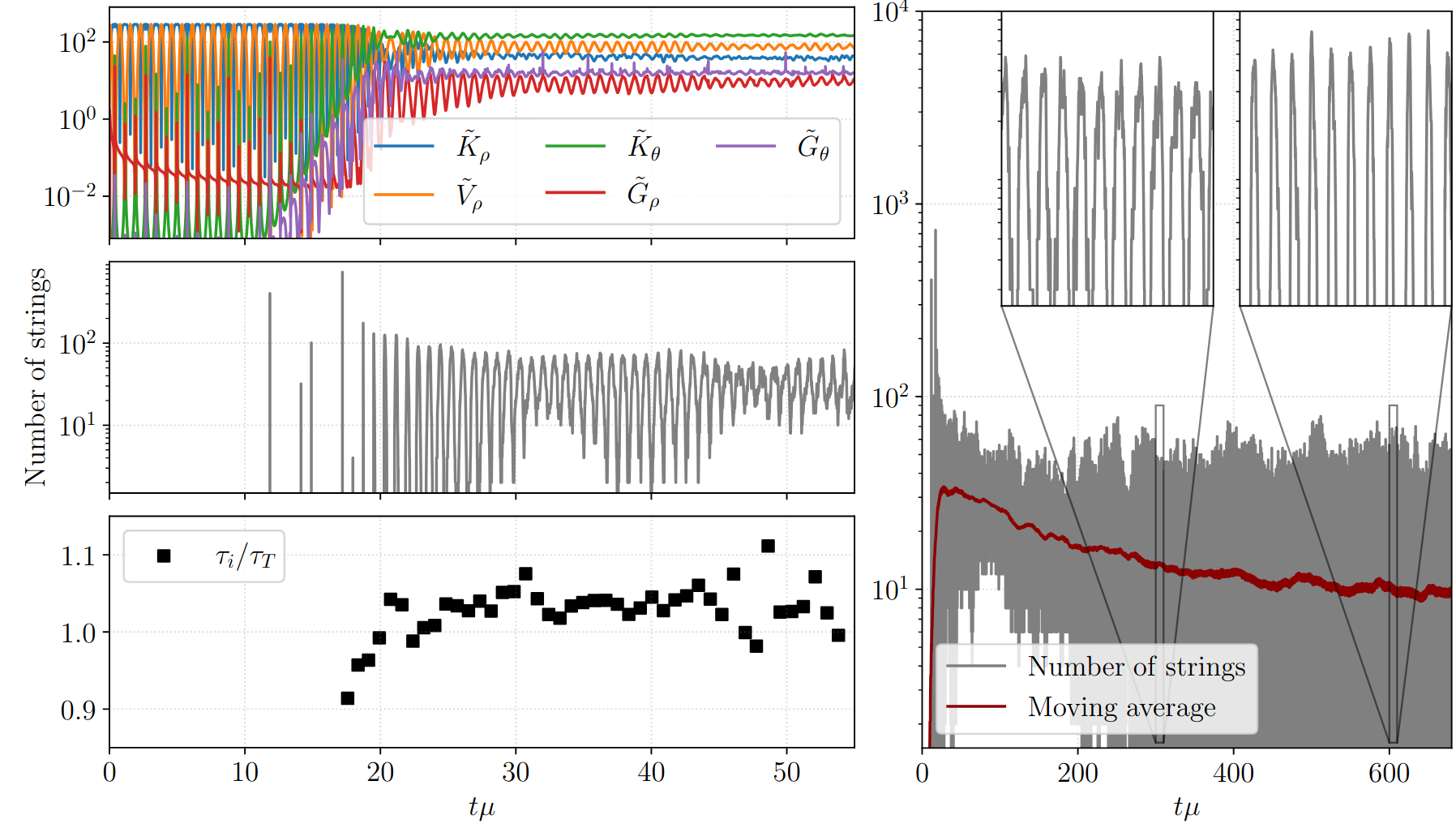
More concretely, the parametric resonance can be seen to drive the gradient energies of both the angular and radial modes (labelled “G” below) in the figure below. This occurs on a coherently oscillating homogeneous background field configuration. Vortex string production becomes efficient only once the modes approach the nonlinear regime. On very long timescales, counter-rotating regions begin to merge, and the number of strings (residing on the boundaries separating counter-rotating regions) decreases. Importantly, the background spacetime is Minkowski in this case:
Fig.: Evolution of the cosmic string number density, the energies associated with the scalar field, as well as a measure of the periodicity of the production bursts of strings after the parametric resonance drove unstable linear modes into the nonlinear regime and the symmetry was locally restored.
Periodic string production occurs both in 2+1 and 3+1 dimensions. In three spatial dimensions, the string nucleates as a loop, expands, and eventually annihilates by shrinking back to a point. This annihilation proceeds efficiently only if the topology of domain boundaries remain unchanged on the timescales of string production. A demonstration of the periodic nature of the string production and complete annihilation is shown in the video below: